Transformation des contraintes en un point dans le cas de l'état plan de contraintes: une définition et deux théorèmes du Dr. Pierre Montès

Depuis plus d'une quinzaine d'années, j'ai, dans mon enseignement de la Résistance des matériaux à des étudiants en génie, introduit une définition et deux théorèmes (nouveaux) qui ne se retrouvent dans aucun livre, sauf dans les cahiers de notes de mes étudiants.

À cause de leur simplicité, je n'ai pas, depuis leur établissement vers 1995-1996, décidé de les publier dans une revue spécialisée. J'ai finalement décidé, aujourd'hui, de les publier sur mon blog, Le Coin de Pierre-Génie civil, pour deux raisons:

1. permettre aux étudiants haïtiens en génie d'avoir accès à cette petite contribution et de l'utiliser dans leurs travaux d'étudiants;
2. permettre à un plus large public d'en profiter.

L'image 1 montre un cube élémentaire centré en un point I d'un solide en équilibre repéré dans un système d'axes direct xyz. On considère le cas particulier où la contrainte normale suivant z est une contrainte principale: l'axe z est une direction principale connue a priori. Et nous considérons les rotations du système d'axes autour de l'axe z seulement.

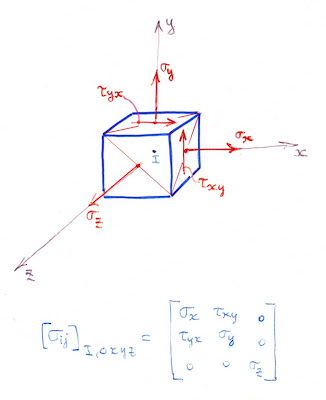
Image 1.- État de contraintes dit «2.5D»
***

Si de plus, la contrainte normale principale suivant l'axe z est nulle, l'état de contraintes au point I est un état plan de contraintes dans le plan x-y.

Pour un angle de rotation «theta» des axes autour de z, le système d'axes devient x'y'z. On considère un nouveau cube élémentaire centré au point I dont les facettes sont perpendiculaires aux nouveaux axes (notez que les plans des facettes de normale z n'ont pas changé, la contrainte normale suivant z non plus). On est intéréssé à déterminer les contraintes normales et tangentielles sur les facettes de normales x' et y', en fonction des contraintes sur le cube dans l'ancien système d'axes et en fonction de l'angle de rotation «theta».

Dans le cas d'un état plan de contraintes, en un point I donné, il existe un angle de rotation «theta» particulier, désigné par «theta_1», pour lequel les contraintes normales sur les facettes de normales x' et y' ne sont pas accompagnées de cisaillement; de plus la contrainte normale suivant l'axe x' est, dans ce cas, la plus grande contrainte normale dans le plan contenant les axes x-y et x'-y', et, la contrainte normale suivant l'axe y' est la plus petite contrainte normale dans le même plan. Les contraintes normales associées au cube dans la direction «theta_1» sont appelées contraintes principales majeure et mineure dans ce plan et dans ce plan seulement.

Ce problème est très classique et est donc traité dans tous les livres de Résistance des matériaux. Il est traité sous «tous» ses angles depuis 1900, c'est-à-dire, depuis l'époque d'Otto Mohr. On peut utiliser soit la solution analytique (équations de transformation des contraintes), soit la solution graphique (cercle de Mohr).

La solution analytique reproduite dans tous les livres de Résistance des matériaux consultés en anglais, en francais, en russe, en roumain, etc., parce qu'elle est basée sur le calcul de l'angle «2 theta_1» à partir de la valeur de sa tangente trigonométrique, malheureusement, conduit à deux solutions (deux angles). Et les auteurs, pourtant de bons ingénieurs, mais des non-mathématiciens, sont «contraints» de dire aux lecteurs et aux étudiants de procéder comme suit pour savoir lequel des deux angles rend maximum (ou minimum) la contrainte normale suivant x': «remplacer l'angle ''2 theta'' successivement par chacune des deux valeurs trouvées pour ''2 theta_1'' dans l'équation de transformation donnant la contrainte normale suivant l'axe x' pour savoir lequel des deux angles choisir pour définir la direction principale majeure».

J'ai toujours été mal à l'aise avec cette façon de faire, car, à l'analyse, il m'apparaissait toujours facile de pouvoir dire a priori, sans nouveaux calculs, lequel des deux angles correspond à la direction principale majeure, comme c'est le cas, quand on utilise le cercle de Mohr pour résoudre le même problème.

Il existe plusieurs manières d'énoncer et d'appliquer la «règle» permettant de savoir, sans nouveaux calculs, lequel des deux angles trouvés correspond à la direction principale majeure (l'autre correspondant à la direction principale mineure dans le plan x-y). Le Théorème 1 est une manière d'énoncer cette «règle».

Sur l'image 2, je présente les équations de transformations des contraintes dans le cas de l'état plan de contraintes dans x-y. Elles se retrouvent dans tous les livres (à une convention de signes près et sous réserve du choix de l'origine de l'angle theta). Elles sont du domaine public: je les ai baptisées (DP1), (DP2) et (DP3) sur l'image 2. Voir par exemple, Bazergui et al. (2002, p. 167-171), Craig (2000, p. 532-539), Lardner et Archer (1994, p. 496-507), Philpot (2008, p. 447-465).

*

***

Image 2.- État plan de contraintes dans le plan x-y: une définition et deux théorèmes du Dr. Pierre Montès

(c) Pierre Montès, 1997, 1998, 1999, 2009
***

Sur l'image 2, j'énonce une Définition importante. J'y définis un angle «2 theta_1» compris entre -180 degrés et +180 degrés. Il est unique sur l'intervalle (une période) choisi; il correspond à un seul point sur le cercle trigonométrique, dont les coordonnées sont un cosinus en abscisses et un sinus en ordonnées, tandis qu'à la définition de l'angle 2 theta_1 des ouvrages de Résistance par la tangente trigonométrique correspondent deux points sur le cercle trigonométrique, ce qui est un peu gênant (gestion plus «lourde»): il faut ensuite déterminer lequel des deux angles correspond à la direction principale majeur. Aucun auteur (à ma connaissance) n'a cherché à contourner cette difficulté.

La définition de l'angle 2 theta_1 que je propose est suivie de deux théorèmes: Théorème 1 et Théorème 2 qui se démontrent très facilement. Je les enseigne à mes étudiants depuis plus de quinze ans à l'École Polytechnique (Montréal).

Le Théorème 1 affirme que l'angle 2 theta_1 obtenu à partir de la Définition rend maximum la contrainte normale suivant l'axe x' incliné de theta-1 sur l'axe x; le Théorème 1 affirme que la contrainte normale suivant l'axe y', perpendiculaire à l'axe x' précédent, est minimum; il affirme, enfin, que la contrainte de cisaillement associée est nulle (cette dernière affirmation n'est pas nouvelle; on le savait déjà; je l'ai ajoutée quoique superflue).

Donc, avec le Théorème 1, il n'est plus nécessaire de substituer chacun des deux candidats pour l'angle 2 theta_1 dans l'équation (DP1) pour savoir lequel des deux rend la contrainte normale suivant l'axe x' maximum (ou minimum).

Le Théorème 2 est une reécriture plus courte des équations (DP1), (DP2), (DP3) en y introduisant l'angle 2 theta_1 qui a une valeur fixée entre -180 degrés et +180 degrés. (On peut choisir d'autres périodes pour définir cet angle; on le sait, il y en a une double infinité).

On établit le Théorème 2 très simplement et très facilement en remplaçant aux seconds membres de (DP1), de(DP2) et de (DP3), la différence des deux contraintes normales et la contrainte de cisaillement par leurs expressions en fonction de R et des lignes trigonométriques tirées des quantités données dans la Définition, et, en utilisant ensuite les identités trigonométriques suivantes dans les expressions trouvées:

cos(a-b) = cos a cos b + sin a sin b

sin(a-b) = sin a cos b - sin b cos a

Les «nouvelles» écritures des équations de transformations des contraintes sont appelées (PM1), (PM2), (PM3).

La démontration du Théorème 2 est indépendante du Théorème 1. Une fois le Théorème 2 démontré, on peut très élégamment et très simplement (sans recours aux dérivées) établir le Théorème 1 en faisant (2 theta) égal à (2 theta_1) dans les formules contenues dans le Théorème 2. C'est ce que j'ai fait en salle de classe cette semaine (9 novembre 2009) dans un cours de Résistance des matériaux donné à des étudiants de Première Année universitaire (deuxième trimestre) ayant déjà suivi un cours de Statique des solides.

La démonstration du Théorème 1 par les dérivées est simple. On annule la dérivée première par rapport à theta de la fonction dans (DP1) et de la fonction dans (DP3) et on montre qu'aux extrema obtenus, la dérivée seconde de la fonction dans (DP1) est négative (condition pour avoir un maximum) et est égale à -4R, tandis que la dérivée seconde de la fonction dans (DP3) est positive (condition pour avoir un minimum) et est égale à +4R. On vérifie aisément que la fonction dans (DP2) s'annule pour la valeur de theta pour laquelle les deux fonctions précédentes atteignent leur extremum respectif.

En guise d'exercices, le lecteur pourra facilement écrire les deux démonstrations suggérées pour le Théorème 1 et la démonstration proposée pour le Théorème 2 en suivant les suggestions et pistes que j'ai données.

Je dois mentionner ici que certains auteurs établissent de manière accessoire, des équations identiques à celles que je déclare «nouvelles», quand ils doivent montrer le lien entre les coordonnées des points X' et Y' du cercle de Mohr et les équations (DP1), (DP2) et (DP3). Mais par la suite, une fois cette preuve faite, ils ne les utilisent plus et ils poursuivent leurs développements à l'aide des équations (DP1), (DP2) et (DP3). Ils semblent n'encourager personne à utiliser ailleurs dans leurs calculs ces équations accessoires.

Ce que je propose ici, avec le Théorème 2, c'est la substitution des équations (PM1), (PM2) et (PM3) aux équations (DP1), (DP2) et (DP3). Ou encore, je propose d'utiliser indifféremment les équations DP et PM, ce que je fais moi-même dans mes travaux et enseignements.

Le Théorème 2 permet aussi de faire clairement et directement le lien entre les trois équations de transformation et le cercle de Mohr.

Le cercle de Mohr est un outil très efficace développé par Otto Mohr en Allemagne (vers 1882). (Avant cette contribution, les ingénieurs devaient analyser les contraintes à l'aide de l'éllipsoïde des contraintes, ce qui est encore valable aujourd'hui, quand on travaille en trois dimensions. Cependant, de nos jours, grâce aux calculatrices et aux ordinateurs, le calcul matriciel s'est imposé comme l'outil par excellence pour l'étude des contraintes en 3D, ce qui simplifie l'écriture des systèmes d'équations linéaires et les calculs associés).

Sur l'image 2 est montrée le cercle de Mohr et le pôle associé. Dans la partie inférieure droite de l'image 2 intitulée: Utilisation du cercle de Mohr, on considère seulement l'un des quatre cas de figure possibles, celui pour lequel la contrainte normale suivant x est supérieure à celle suivant y, et, la contrainte de cisaillement qui les accompagne est prise positive. De plus, on a considéré le cas où les contraintes normales suivant x et y sont positives.

On rappelle ici la convention de signes pour les facettes et pour les contraintes.

Facettes: Sur un cube repéré dans un système d'axes direct xyz, une facette dont la normale unitaire extérieure est de même sens qu'un axe du système est dite positive; elle est négative dans le cas contraire.

Contraintes: Sur un cube repéré dans un système d'axes direct xyz, une contrainte agissant sur une facette positive et dirigée dans le sens positif d'un axe du système est positive; elle est négative si elle est dirigée dans le sens négatif d'un axe sur une facette positive. De même, une contrainte agissant sur une facette négative et dirigée dans le sens négatif d'un axe du système est positive; elle est négative si elle est dirigée dans le sens positif d'un axe sur une facette négative.

Pôle: L'utilisation du pôle permet de mener des parallèles aux facettes au lieu de faire des rotations d'angles, ce qui facilite encore plus l'utilisation du cercle de Mohr. La parallèle à une facette menée par le pôle rencontre le cercle en un second point dont les coordonnées sont les composantes des contraintes agissant sur cette facette. Pour obtenir au préalable le pôle, il suffit de mener par les points X et Y diamétralement opposés qui ont servi à tracer le cercle de Mohr des parallèles aux facettes de même nom: l'intersection de ces deux droites est un point du cercle: c'est le pôle.

Construction du cercle de Mohr dans le plan x-y (Rappel): Le plan x-y contenant les facettes du cube sur lesquelles sont représentées les contraintes normales et tangentielles est ordinairement appelé plan physique. Sur la même page que le plan physique, on trace le plan de Mohr pour faciliter le passage (ou la correspondance) de l'un à l'autre. En Résistance des matériaux (voir les références fournies à la fin), on prend l'habitude de tracer dans le plan de Mohr l'axe des contraintes normales horizontal et orienté vers la droite (traction positive, compression négative); l'axe des cisaillement lui est perpendiculaire et orienté vers le bas. (Cette façon de faire est directement liée à la convention de signes que l'on s'est donnée ici. Si l'on change de convention, il se peut que le sens de l'axe du cisaillement soit changé. Faites bien attention si vous utilisez plusieurs ouvrages de résistance à la fois. Si tel est le cas, prenez le temps de vérifier quelle convention chaque auteur utilise pour les contraintes normales et les contraintes de cisaillement, d'une par, et, d'autre part, comment il définit l'angle theta qui entre dans ses équations de tranformations. Rappelez-vous que le matériaux ne connait pas de convention de signe, lui; il répond (se déforme) suivant la sollicitation qui lui est appliquée. Toutes les conventions mènent aux mêmes réponses (déformations) que subit par le matériau).

On définit et on place deux points X et Y sur le plan de Mohr. Le point X a pour coordonnées: la contrainte normale suivant l'axe x du plan physique avec son signe; la contrainte de cisaillement qui l'accompagne sur le plan physique avec son signe sur le plan physique. Le point Y a pour coordonnées: la contrainte normale suivant l'axe y du plan physique avec son signe; la valeur numérique opposée de celle de la contrainte de cisaillement qui l'accompagne dans le plan physique. Voici une règle (infaillible, si elle est bien suivie) permettant de vérifier si les points X et Y sont bien placés sur le plan de Mohr. Considérons dans le plan physique une contrainte de cisaillement agissant sur une facette du cube (celle de normale x, ou celle de normale y). Considérons un point à l'intérieur du cube. Si cette contrainte de cisaillement était une force, on détermine quel serait le sens du mouvement de rotation que causerait au cube, le moment de cette force fictive seule par rapport au point choisi. Si le sens de la rotation ainsi obtenu est anti-horaire (trigonométrique), on porte la valeur du cisaillement dans la partie inférieure (positive ici) de l'axe du cisaillement dans le plan de Mohr. Si le sens de la rotation est le sens horaire (celui des aiguilles d'une montre), on porte la valeur du cisaillemet dans la partie supérieure (négative ici) de l'axe du cisaillement dans le plan de Mohr. On peut vérifier que cette règle a été appliquée pour les points X et Y du cercle de Mohr tracés sur l'image 2 ci-dessus.

Les points X et Y étant placés dans le plan de Mohr, ils constituent les extrémités d'un diamètre du cercle de Mohr, le diamètre XY. L'exploitation du cercle de Mohr se fait ensuite soit à l'aide du pôle, soit à l'aide de la rotation du diamètre XY. À une rotation d'un angle theta du système x-y autour de l'axe z du plan physique pour devenir x'y', correspond une rotation dans le même sens mais d'un angle double (2 theta) du diamètre XY dans le plan de Mohr. Les angles theta du plan physique sont mesurés à partir de l'axe de référence x (rotation positive si effectuée dans le sens trigonométrique); les angles 2 theta dans le plan de Mohr sont mesurés à partir du rayon de référence qui joint le centre du cercle au point X. Comme dit précédemment, l'utilisation du pôle permet de mener dans le plan de Mohr des parallèles aux facettes du plan physique plutôt que de faire des rotations d'angles.

________________

Notes

1. Je dois mentionner que dans l'établissement des équations (PM1), (PM2) et (PM3) ainsi que dans la formulation de la Définition, j'ai usé de mes vieux souvenirs du cours de Physique de classes terminales (courant alternatif, angle de déphasage, triangle de Fresnel...) comme source de motivation.
2. Dès 1995-1996, j'ai énoncé une définition et démontré deux théorèmes, semblables à ceux présentés ici, pour l'étude de l'état plan de déformations (ce qui est évident, les contraintes et les déformations étant liées linéairement (loi de Hooke généralisée)).
3. Dès 1995-1996, j'ai énoncé une définition et deux théorèmes, semblables à ceux présentés ici, pour l'étude de l'état plan de contraintes (ou de déformations) en Mécanique des sols.
4. Dès 1995-1996, j'ai énoncé une définition et deux théorèmes, semblables à ceux présentés ici, pour l'étude de la transformation des (moments d'inertie) seconds moments de surfaces (Ix, Iy et Ixy) en (Ix', Iy' et Ix'y'), très utiles dans la théorie des poutres fléchies.
5. L'étude du problème en trois dimentions (contraintes, déformations ou moments d'inertie) est traitée dans des cours avancés de RDM. Elle est malheureusement peu ou pas enseignée au premier cycle universitaire ! J'ai enseigné ces notions au premier cycle à des étudiants inscrits dans un programme de génie civil durant les deux premiers tiers de la décennie 1990. L'étude des contraintes et des déformations en trois dimensions permet une compréhension plus globale et plus complète de l'état de contraintes (ou de déformations) en un point. Les notions de mathématiques que cet enseignement nécessite sont déjà très bien maîtrisées par les étudiants (algèbre linéaire, analyse mathématique). Il n'y a donc aucunes raisons qui justifient l'exclusion de l'enseignement de ces notions avancées de Résistance des Matériaux aux étudiants du premier cycle universitaire. J'ai écrit et utilisé des notes de cours et un recueil de problèmes pour l'étude de la Résistance des matériaux en trois dimensions. Si un jour, cet enseignement redevenait populaire au premier cycle, alors, je serais encouragé à publier ces deux documents.

___________________________

Quelques références:

1. Bazerghi, A., Bui-Quoc, T., Biron, A., McIntyre, C. (2002), Résistance des matériaux, troisième édition, Presses internationales Polytechnique, 715 p.
2. Craig, R.R. (2000), Mechanics of materials, second edition, John Wiley and Sons, 752 p. and Appendixes (or Appendices).
3. Lardner, T.J. and Archer, R.R. (1994), Mechanics of Solids, An Introduction, McGraw-Hill, 802 p.
4. Philpot, T.A. (2008), Mechanics of Materials, An Integrated Learning System, John Wiley and Sons, 718 p.